"Real-world" example: Heat diffusion¶

Note: This should be run with multiple Julia threads (I recommend 8 on Noctua 2)

The heat equation¶

We consider the heat equation, a partial differential equation (PDE) describing the diffusion of heat over time. The PDE reads

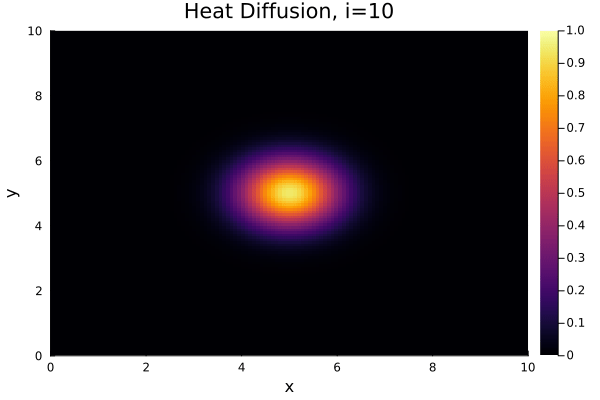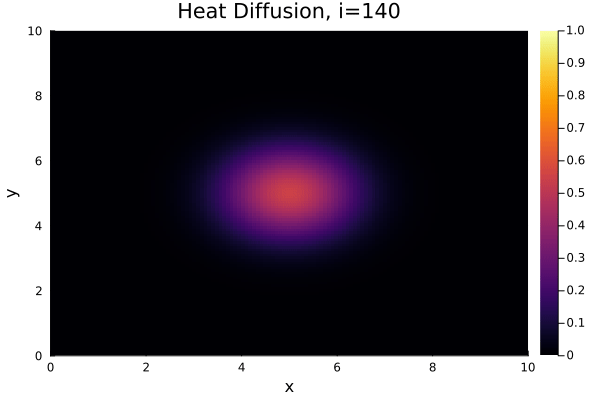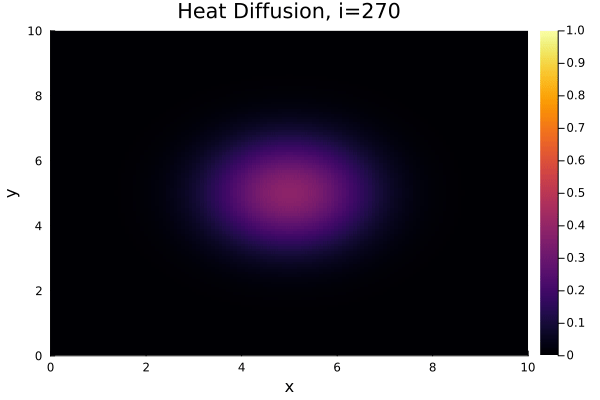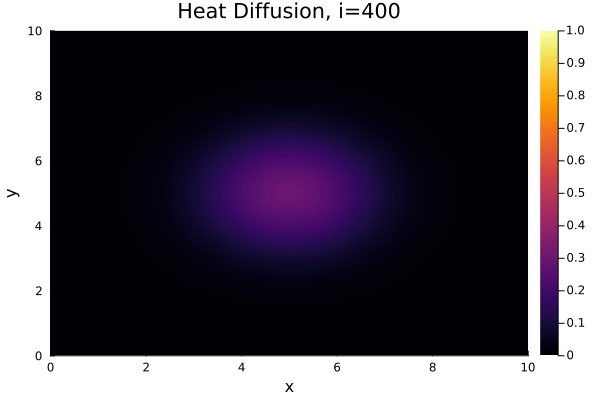
$$ \dfrac{\partial T}{\partial t} = \alpha \left( \dfrac{\partial^2 T}{\partial x^2} + \dfrac{\partial^2 T}{\partial y^2} \right), $$

where the temperature $T = T(x,y,t)$ is a function of space ($x,y$) and time ($t$) and $\alpha$ is a scaling coefficient. Specifically, we'll consider a simple two-dimensional square geometry. As the initial condition - the starting distribution of temperature across the geometry - we choose a "Gaussian" positioned in the center.

Numerical solver¶

  1. We discretize space (dx, dy) and time (dt) and evaluate everything on a grid.
  2. We use the basic finite difference method to compute derivatives on the grid, e.g.
$$ \dfrac{\partial T}{\partial x}(x_i) \approx \dfrac{f(x_{i+1}) - f(x_i)}{\Delta x} $$
  1. We use a two-step process: a) Compute the first-order spatial derivates. b) Then, update the temperature field (time integration).
$$ \begin{align} \partial x &= \dfrac{\Delta T}{\Delta x} \\ \partial y &= \dfrac{\Delta T}{\Delta y} \\ \Delta T &= \alpha\Delta t \left( \dfrac{\Delta (\partial x)}{\Delta x} + \dfrac{(\Delta \partial y)}{\Delta y} \right) \end{align} $$

Note that the derivatives give our numerical solver the character of a stencil. Stencils are typically memory bound, that is, data transfer is dominating over FLOPs and consequently performance is limited by the rate at which memory is transferred between memory and the arithmetic units. For this reason we will measure the performance in terms of an effective memory bandwidth.

Result¶

Implementation¶

In [4]:
using Printf
using Base.Threads: @threads, nthreads

Base.@kwdef struct Parameters
    Δ::Float64
    Δt::Float64
    ngrid::Int64
end

function compute_first_order_loop_mt!(∂x, ∂y, T, p)
    @threads :static for j in 2:(p.ngrid-1)
        for i in 1:(p.ngrid-1)
            @inbounds ∂x[i, j-1] = (T[i+1, j] - T[i, j]) / p.Δ
        end
    end
    @threads :static for j in 1:(p.ngrid-1)
        for i in 2:(p.ngrid-1)
            @inbounds ∂y[i-1, j] = (T[i, j+1] - T[i, j]) / p.Δ
        end
    end
    return nothing
end

function update_T_loop_mt!(T, ∂x, ∂y, p)
    @threads :static for j in 2:(p.ngrid-1)
        for i in 2:(p.ngrid-1)
            @inbounds T[i, j] = T[i, j] + p.Δt *
                                          ((∂x[i, j-1] - ∂x[i-1, j-1]) / p.Δ +
                                           (∂y[i-1, j] - ∂y[i-1, j-1]) / p.Δ)
        end
    end
    return nothing
end

function heatdiff_multithreading(; ngrid=2^12, init=:serial, timesteps=400, verbose=true)
    L = 10.0 # domain length
    Δ = L / ngrid # domain discretization
    Δt = Δ^2 / 4.1 # time discretization
    pts = range(start=Δ / 2, stop=L - Δ / 2, length=ngrid)
    p = Parameters(; Δt, Δ, ngrid)

    # temperature field - initial condition
    T = Matrix{Float64}(undef, ngrid, ngrid)
    if init != :parallel
        T .= exp.(.-(pts .- L ./ 2.0) .^ 2 .- (pts .- L ./ 2.0)' .^ 2)
    else
        @threads :static for j in axes(T, 2)
            for i in axes(T, 1)
                T[i, j] = exp(-(pts[i] - L / 2.0)^2 - (pts[j] - L / 2.0)^2)
            end
        end
    end

    # partial derivatives (preallocation)
    ∂x = Matrix{Float64}(undef, ngrid - 1, ngrid - 2)
    ∂y = Matrix{Float64}(undef, ngrid - 2, ngrid - 1)
    if init != :parallel
        fill!(∂x, 0.0)
        fill!(∂y, 0.0)
    else

        @threads :static for j in axes(∂x, 2)
            for i in axes(∂x, 1)
                ∂x[i, j] = 0.0
            end
        end

        @threads :static for j in axes(∂y, 2)
            for i in axes(∂y, 1)
                ∂y[i, j] = 0.0
            end
        end
    end

    # time loop
    elapsed_time = @elapsed for _ in 1:timesteps
        # -------- stencil kernel --------
        # first order derivatives
        compute_first_order_loop_mt!(∂x, ∂y, T, p)
        # update T
        update_T_loop_mt!(T, ∂x, ∂y, p)
        # --------------------------------
    end
    membw_eff = 2 * ngrid^2 * sizeof(eltype(T)) * timesteps * 1e-9 / elapsed_time
    if verbose
        @printf("\tResults: membw_eff = %1.2f GB/s, time = %1.1e s \n", round(membw_eff; digits=2), elapsed_time)
    end
    return membw_eff
end
Out[4]:
heatdiff_multithreading (generic function with 1 method)

Benchmark¶

In [5]:
using ThreadPinning
using PrettyTables

function bench(; nrepeat=1, ngrid=2^12)
    # measurements
    membw_results = Matrix{Float64}(undef, 3, 2)
    for (i, pin) in enumerate((:cores, :sockets, :numa))
        for (j, init) in enumerate((:serial, :parallel))
            pinthreads(pin)
            membw = 0.0
            for _ in 1:nrepeat
                membw = max(heatdiff_multithreading(; init, ngrid, verbose=false), membw)
                # membw += heatdiff_multithreading(; init=init, verbose=false)
            end
            # membw /= nrepeat
            membw_results[i, j] = round(membw; digits=2)
        end
    end

    # (pretty) printing
    println()
    pretty_table(membw_results;
        header=[":serial", ":parallel"],
        row_names=[":cores", ":sockets", ":numa"],
        row_name_column_title="# Threads = $(Threads.nthreads())",
        title="Effective Memory Bandwidth (GB/s)")
    return nothing
end

bench()

Effective Memory Bandwidth (GB/s)
┌───────────────┬─────────┬───────────┐
│ # Threads = 8 │ :serial │ :parallel │
├───────────────┼─────────┼───────────┤
│        :cores │    7.49 │      7.53 │
│      :sockets │    8.77 │     17.91 │
│         :numa │   17.19 │     71.48 │
└───────────────┴─────────┴───────────┘